As part of the ordeals of saving bubbly, we also learnt three simple yet powerful ways to sort a bunch of elements. Bubble sort, Selection sort and Insertion sort. It is only human nature to compare stuff when you have multiple options.
But before we start comparing different algorithms, we need to set some rules. Until now we tried to keep the complexity out of our equations and we will continue to do so as far as we can, but its a fair wish to compare our options.
All work and no play makes Jack a dull boy. But all play and no work also seems to do the same. :) So for a change, this time its going to be a dam serious affaire. Bite me if I smile here after or let you smile. The fact is, I tried so hard to find a funny way to explain this complexity stuff but I could not. I will still continue to find a funny way to understand this stuff but until then, let's be serious as hell.
Welcome to the space time Continuum ...
When we write a program or an algorithm, our primary goals are:- It does what its supposed to do.
- It is able to identify the error situations and is able to handle them properly.
But that's just scratching the surface. In our normal Hello world program and almost 90% of real life programs, that just might be fine, but when it comes to real life complex and large scale applications, few things become more critical. Some times even if the program does what it is supposed to do, that's just not enough and it must be seen:
- How much space will this program consume at runtime.
- How much time will it take to complete the execution.
Space Complexity:
When a program executes, we are concerned about:
- How much space will it take on the stack (method calls and local variables)
- How much space will it take on the heap (Objects and their references)
The stack space is fairly simple and we would not focus on it as much. We will calculate the heap space as that's what matters the most and is dependent on how we write our code and what are the inputs to the code.
The space complexity can simply be defined by the following equation:
Space complexity = Sum of space needed for total number of objects created + space needed for references
Time Complexity:
The time complexity can simply be defined by the following algorithm:
Start with count = 0.
for each step executed in a program, increase count like:
for each step
count = count +1;
But an important thing to consider while calculating these complexities is that based on the input factor, the algorithm may at times perform at its BEST while at other times, it may perform at its WORST
Be it time or space, as programmers I think, for us its more important to calculate how much maximum time or memory our program would take so that we can plan our resources accordingly. So we will mostly focus on the Worst case scenario here. Also, At this point, we will only focus on the time part of it as for the programs we will write for a while, our personal computer's memory would be much more than enough and we won't run out of it.
Asymptotic Notations:
Asymptotic means approaching a value or curve arbitrarily closely (some sort of limit). As mentioned earlier, we are only preparing for the worst. So we will only discuss the asymptotic notation that describes the worst case time complexity of an algorithm.Big-O
As already discussed, and which will be more clear when we compare our efforts to save Bubbly, how much time and algorithm will take largely depends on the input we provide to the algorithm. For simplicity, we would go further and say it largely depends on the size of the input to the algorithm.So if I say that the time needed for the execution of an algorithm is a function of the size of input to the algorithm, I hope it would not be too much of math here.
so I can say:
Time complexity = f(n)
Now, Big-O notation represents the worst case time an algorithm can take. Its an asymptotic notation, which means it will represent the complexity like approaching to some value. As its worst case scenario, Big-O will represent the maximum time an algorithm can take.
so I can say:
Worst case Time complexity = O (g(n))
So I can say, at all times:
f(n) <= C * g(n)
where C is the constant time representing steps that are not directly dependent on the input.
With this background, lets analyze how we did in our three attempts to save bubbly.
Bubble sort
As you can see in the post Operation rescue Bubbly... in the first pass through Bubbly's stomach, we did 4 comparisons, in the second pass we did 3 comparisons and so on down to 1 comparison on the last pass. For 5 chocolates, this was:
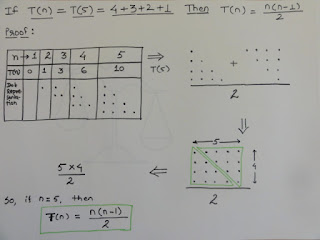
4+3+2+1 = 10
lets generalize it. So if Bubbly had eaten n chocolates, it would be:
(n-1)+(n-2)+(n-3)...+1 = n*(n-1)/2
The -1 here does not make much sense, specially if n becomes quite large. So we can say that the algorithm does n^2/2 comparisons.
There were less swaps than comparisons as two chocolates were swapped only when needed. But for our worst case scenario, lets assume there was a swap for each comparison. so we have n^2/2 swaps.
As can be seen in the above definition of Big-O notation, constants are ignored, so we can say:
Time complexity of bubble sort = O(n^2)
Selection sort
When Bubbly did the mistake again in a silly mistake..., we tried to find a way to save bubbly with some less pain to her. What we did was try to use selection sort on her stomach. Though the number of comparisons we did were the same, we saved some effort on the painful swapping part. The saving on swapping is actually a great deal if the number of elements is large.
As you must have seen, in each pass through Bubbly's stomach, we did only one swap if at all. In a worst case scenario, there would be exactly one swap for each pass, so in general for 5 chocolates, there would be 10 comparisons but less than 5 swaps, if there were 10 chocolates, there would be 45 comparisons but less than 10 swaps.
As there are O(n^2) comparisons needed to complete the sort, the overall complexity of the algorithm still stays O(n^2), but selection sort is undoubtedly faster than bubble sort as it requires very few swaps.
Insertion sort
This one is the best so far. The overall complexity of insertion sort is also O(n^2) thanks to the comparisons on each pass, but its almost twice as fast as bubble sort and a little faster than selection sort. Lets find out how:
The very first reason it is faster than the other two is that it does not do a swap at all. It does a copy which is faster than a swap. Secondly, the comparisons done are on a sorted array. So in the first pass, it does a comparison on 1 item, in the second pass it does a comparison on 2 items and so on up to n-1 items. So in a worst case there are n(n-1)/2 comparisons.
As can be seen from Bubbly's ordeal in Las Vegas: Bubbly goes to Las Vegas..., we needed only 3 copies when we moved 2,4 and A to their deserved positions respectively. But in most real life situations on an average, about a half of the items need to be compared and copied, before an insertion point for the next sorted candidate is found, making the algorithm faster than the other two in real life situations as well.
So after all, gambling is a good thing. It taught you how to sort numbers the fastest. But hold your horses there, these sorting algorithms are just scratching the surface. There are lot faster algorithms out there waiting for our exploration.
I hope this article was as boring to you as I expected it to be.
As usual, comments/appreciation/criticism(a constructive one of course) everything is most welcome and appreciated.
Until then,
Happy Learning!
Banyan Bat

No comments:
Post a Comment